How To Draw A Dart Board
This post will comprehend the steps required to draw a traditional Dartboard using HTML5's canvas. The final product produces the post-obit rendered board.
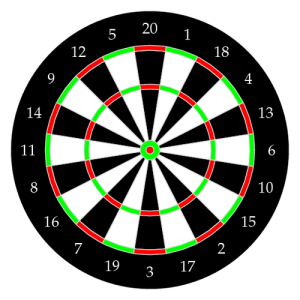
To tackle this task one'due south thought process was to picture how one would depict a dartboard using layers. In theory you lot would start by drawing the blackness circle that forms the base of operations of the board. Followed by the alternating black and while pie sections. The double and treble arcs would then exist placed accordingly, followed by the outer-balderdash and bulls-eye circles. And finally, the wire-works between the pie sections and lettering on the outer ring.
A working version of the above tin can be viewed Dart board Canvas. The HTML markup to create this folio consists of the following:
<html lang="en"> <head> <meta charset="utf-eight" /> <title>Elementary Canvas Dartbaord</championship> <script src='./victor.min.js'> <canvas id="sail" width="400" height="400"></canvas>
The higher up code snip-information technology includes ii important parts. This first part is the inclusion of the HTML5 sheet tag and the surrounding HTML elements. This forms the foundation of the page. The canvas tag is used to draw the board. The logic to draw the board is driven by the JavaScript lawmaking. This is the second part. Information technology can exist found within the files included by the script tags e.thou.
<script src='./victor.min.js'>
The victor.js file brings is a mathematical library which provides a prepare of Vector based functions. This is used to summate the x and y positions of the various points of the board. The second script provides the master logic for drawing onto the canvas.
The whole drawing processes is started when the first fleck of JavaScript is executed. This tin can be constitute inside 'onload' result of the page:
<body onload='DartBoard().init();'>
Drawing the blackness base of the board is fairly petty. Information technology is accomplished using the arc function which is provided by the canvass API:
function drawCircle(radius, colour, fillColour) { ctx.beginPath(); ctx.arc(center.x, center.y, radius, 0, two * Math.PI, imitation); ctx.lineWidth = one; ctx.strokeStyle = color; if(fillColour) { ctx.fillStyle = fillColour; ctx.fill(); } ctx.stroke(); } The code above is a utility function. It takes three parameters. The first is the radius of the circle. The 2nd and third are the colour attributes. One for the outer edge and the other for the fill circle. In this instance the center point of the dartboard is stock-still. This is prepare once when the draw office starts.
The base board, outer and inner rings (including the bulls-middle) all share the same center point. The only differing factor is the colour of the circles that make upwardly the board and the radius of each. Using the higher up utility role nosotros first draw the base board (and later the inner and out bull).

The adjacent step is to draw the first pie segment. This is the segment representing the part which would score you xx points. To understand how we achieve this we first demand to suspension the board down mathematically. We know that the board is split into twenty pie-sliced shaped areas and a circumvolve consists of iii-hundred and threescore degrees. Dividing three-hundred and lx past twenty will give united states of america the portion of the circle that one pie sliced takes: a value of xviii degrees. The center of the first segment is positioned at cypher degrees. Nosotros need to draw our first segment starting at three-hundred and sixty minus half the size of one segment (viii). The stop of the segment is this value plus eighteen. Drawing this segment give us:

The following code will depict all of the twenty segments:
for(counter = -nine; counter < (360 - 9); counter += PIECES) { buildRing(doubleTopMin, doubleTopMax, counter, counter + PIECES, count++ % two ? 'cerise' : '#03ff03'); buildRing(tripleMin, tripleMax, counter, counter + PIECES, count % 2 ? '#03ff03' : 'red'); buildRing(doubleTopMin, tripleMax, counter, counter + PIECES, count % 2 ? 'white' : 'blackness'); buildRing(tripleMin, twentyFiveTopMin, counter, counter + PIECES, count % 2 ? 'white' : 'black'); printLabel(counter, pos++); } This outcome in:

Every bit you can see from the higher up image the board is nigh complete. In the loop there are only two function calls. The start is called 'buildRing' and the 2nd 'printLabel'. The 'buildring' function again uses bones vector maths to calculate the coordinates (10 and y) required to describe each of the segments. Each segment consists of four sections. Theses are the double top, upper fat, triple and lower parts. The 'buildring' utility function takes the upper and lower bound of each and draws the segment using the colour supplied. The code for this is:
function buildRing(min, max, startDeg, endDeg, colour) { ctx.beginPath(); ctx.fillStyle = color; ctx.strokeStyle = colour; for(var counter = startDeg; counter <= endDeg; counter += one) { var doubleTopMaxPoint = centerVector .clone() .add(lengthVector .clone() .norm() .rotateDeg(counter) .multiply(new Victor(max, max)) ); ctx.lineTo(doubleTopMaxPoint.x, doubleTopMaxPoint.y); } for(counter = endDeg; counter >= startDeg; counter -= one) { var doubleTopMinPoint = centerVector .clone() .add(lengthVector .clone() .norm() .rotateDeg(counter) .multiply(new Victor(min, min)) ); ctx.lineTo(doubleTopMinPoint.x, doubleTopMinPoint.y); } ctx.fill up(); ctx.stroke(); } This utility function loops around; moving one caste at a fourth dimension from left to right forth the top of the segment. Each point is passed to the lineTo role (a sail API function). Information technology then repeats this in the second loop; but, goes correct to left for the lesser of a segment. At the end of this, the points calculated grade a path. This path is filled with the advisable colour forming the full segment block.
The other utility function is the 'printLabel' role:
function printLabel(counter, pos) { var labels = [ 20, 1, 18, 4, 13, 6, 10, 15, 2, 17, three, nineteen, 7, 16, 8, eleven, 14, 9, 12, 5 ]; var firstWireOfPeice = counter + 9; var x = centerVector .clone() .add(lengthVector .clone() .norm() .rotateDeg(firstWireOfPeice) .multiply(new Victor(doubleTopMax, doubleTopMax)) ); var adapt; if (firstWireOfPeice < 55 || firstWireOfPeice > 295) { adjust = new Victor(radius - 10, radius - 10); } else if (firstWireOfPeice > 95 && firstWireOfPeice < 265) { adjust = new Victor(radius + 10, radius + ten); } else { conform = new Victor(radius, radius); } var edge = centerVector .clone() .add(lengthVector .clone() .norm() .rotateDeg(firstWireOfPeice) .multiply(adjust) ); drawLabel(labels[pos], edge, ten); } This function begins past declaring an array of scores. The parameters passed into the function represents the alphabetize (or counter) of the label to depict and the position in degrees of the start of the segment. Over again using a simple fleck of vector math the labels position is calculated. This position is then used to draw the label.
The penultimate role of the lawmaking is the cartoon of the metal wire-works which divide each segment. This is done within the 'drawRadials' role:
role drawRadials() { ctx.lineWidth = two; ctx.strokeStyle = 'white'; for(counter = nine; counter < 360; counter += PIECES) { var get-go = new Victor(0, 10); 10 = centerVector .clone() .add(lengthVector .clone() .norm() .rotateDeg(counter) .multiply(new Victor(doubleTopMax, doubleTopMax)) ); drawRadial(10); } function drawRadials() { ctx.lineWidth = ii; ctx.strokeStyle = 'white'; for(counter = 9; counter < 360; counter += PIECES) { var offSet = new Victor(0, 10); x = centerVector .clone() .add(lengthVector .clone() .norm() .rotateDeg(counter) .multiply(new Victor(doubleTopMax, doubleTopMax)) ); drawRadial(x); } } }</pre> <pre> The first function 'drawRadial' simply repeats the loop discussed above. Withal, this time we simply draw a silver line from the center of the board to the outer limit of the double band. Drawn on it ain produces the following:

And finally, we depict the inner and outer bull area. I left this until last as it overlays the center area and thus, hides the parts of the silver radials that we practise non want to run into. The inner, outer bull and its wire-work are fatigued using the following:
drawCircle(doubleTopMax, 'silver'); drawCircle(doubleTopMin, 'silver'); drawCircle(tripleMax, 'silver'); drawCircle(tripleMin, 'argent'); drawCircle(twentyFiveTopMin, 'silver', 'light-green'); drawCircle(bullTopMin, 'silver', 'crimson');
As y'all can run into this simply calls the 'drawCircle' office. Passing in the radius at which the circles should be fatigued and their appropriate colours. This result in the final render the board:

That concludes one's experiment with sport :-). I hope this helps someone out there. A working version of the above can be viewed HTML5 Canvas dartboard. If you have any feedback please comment below. This is as well available at my git repository HTML5 goodies.
Source: https://geeksretreat.wordpress.com/2015/10/14/how-to-draw-a-dartboard-using-htmls-canvas/
Posted by: sellarsvate1986.blogspot.com


0 Response to "How To Draw A Dart Board"
Post a Comment